Bhabha散乱とは
「また、異なる基準座標系を用いた計算も容易になる。例えば、振幅と散乱断面積との間の関係を示す(1.1)式の修正のみで事足りる。
散乱の微分断面積:

「あるいは、重心系の計算により得られた結果に、単純にローレンツ変換を行うこともできる。始状態および/または終状態の粒子のスピン状態が既知であり、ミュー粒子の質量を考慮したい場合は、計算はすこし面倒になるけど、原理的にまったく難しいことはない。ファインマン・トレース技術は、このような場合に一般化できるけど、スピノルおよび
の明確な値を用いて(1.10)式を直接評価することもしばしば容易になる」
「次に、異なるプロセスの散乱断面積も計算できる。例えば、のプロセスは、Bhabha散乱として知られる」
「ぶはぶは散乱?」
「バーバー散乱と発音する。インドの原子力開発の立役者であるホーミ・J・バーバー(Homi Jehangir Bhabha)に因む。Bhabha散乱は、一言で言えば、電子ー陽電子散乱のこと。図1.6は、Bhabha散乱の最低次の2つのファインマン図を示す」
図1.6
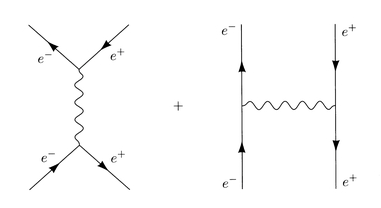
「図1.6に示すように、Bhabha散乱は、2通りの場合が考えられるため、計算がより難しくなる」
「電子と陽電子が対消滅して仮想光子を放出する場合と、電子と陽電子が対消滅せずに仮想光子を交換する場合の2通りの場合があるわけね」
「実際の計算では、これら2つのファインマン図で求めた振幅を足し合わせた後で二乗する」
Bhabha散乱(以下の2通りの過程を考慮する)
1.電子と陽電子が対消滅して仮想光子を放出し、仮想光子を吸収して再び電子と陽電子対が生成される
2.電子と陽電子が仮想光子を交換して相互作用する
「もう1つのプロセスは、コンプトン散乱。コンプトン散乱は、X線(光子)を物質(電子)に当てたとき、散乱されたX線の波長が入射したX線の波長よりも大きくなる現象。図1.7は、コンプトン散乱の最低次の2つのファインマン図を示す」
図1.7
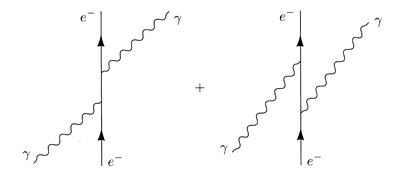
「図1.7に示すように、電子が仮想光子を吸収して放出する場合と、電子が仮想光子を放出して吸収する場合の2通りの場合が考えられる」
コンプトン散乱(以下の2通りの過程を考慮する)
1.電子が仮想光子を吸収して放出する
2.電子が仮想光子を放出して吸収する
「電子が先に仮想光子を放出する場合も含まれているわけね」
「コンプトン散乱については、セクション5.5で詳細を議論するらしい」