複素積分における積分路の変形 - スーパーサイエンスガール

「次に、空間的なクライン‐ゴルドン場の伝搬粒子の振幅の具体的な値を計算してみましょう」

${ \displaystyle \begin{eqnarray} D(x-y)&=&\int\frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bf{p}}}e^{i{\bf{p}\cdot\bf{r}}}\\ &=&\frac{2\pi}{(2\pi)^3}\int_0^\infty dp\frac{p^2}{2E_{\bf{p}}}\frac{e^{ipr}-e^{-ipr}}{ipr}\\ &=&\frac{-i}{2(2\pi)^2r}\int_{-\infty}^\infty dp\frac{p e^{ipr}}{\sqrt{p^2+m^2}}. \end{eqnarray} }$

「上式の被積分関数 $\frac{p e^{ipr}}{\sqrt{p^2+m^2}}$ を複素関数に拡張して考えると、図2.3に示されるように、 $\pm im$ から始まる虚軸上の分岐（ぶんき）（branch cut）を有します」

f:id:Dreistein:20150613083017p:plain
図2.3 空間的距離上の伝搬関数D(x-y)を評価するための積分路

「ここで、上の積分を評価するために、上の分岐のまわりを覆うように、積分路（contour）を上方に押し上げます（push the contour upward）。複素平面上の積分（複素積分）においては、正則でない点、すなわち特異点を含まない限り、自由な積分路を選んで積分することができます」
「自由な積分路？　どんな積分路でもいいの？」
　一宮が胡散臭そうな目で越野さんを見た。
「どんな積分路でもいいわけではありません。例えば、積分路が、自由に伸び縮みする『ひも』のようなものであり、特異点が、複素平面上に固定された『釘』のようなものであるとイメージしてください。釘に引っかからない限り、ひもを自由に変形することができますよね。それと同じように、複素平面上の積分路も、特異点を横切らない限り、自由に変形することができるのです」

積分路→自由に伸び縮みするひも
特異点→複素平面上に固定された釘
　↓
釘（特異点）にひっかからない限り、ひも（積分路）を自由に変形することができる

f:id:Dreistein:20150613090729p:plain

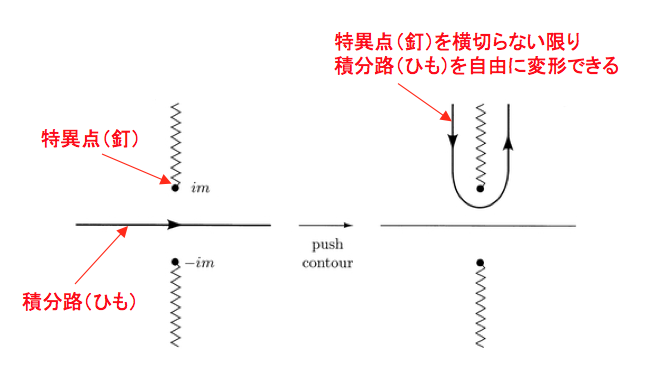
「特異点は、被積分関数がゼロになる点、すなわち、 $z=\pm im$ の点なので、この特異点を横切らない限りは、積分路を自由に変形することができます。ちょうど、まっすぐ水平に伸びていたひもの両端を、位置 $z=im$ の釘をはさむように上方に伸ばすことによって、新たな積分路を作ることができるのです」
「いくらなんでも、それは変形しすぎじゃない？」
「上の性質は、次のコーシーの積分定理から厳密に導かれるので問題ありません」

コーシーの積分定理
関数f(z)が単一の閉曲線CとCの内部を含む領域で正則であるとき、閉曲線C上の線積分が0になる
${ \displaystyle \begin{eqnarray} \oint_Cf(z)dz=0 \end{eqnarray} }$

「ちなみに、このテキストでは、複素平面上の積分路の変形を『push the contour upward』と表現しているようです」
「そういえば、今年の初め頃だったかしら。相対論的な粒子の確率振幅について似たような計算をしたわね。ひょっとすると、あのときの積分計算も、本当はこんな感じに積分路を変形するんじゃなかったんじゃないの？」
　一宮は、石原をにらみつけた。

　そういえば、そのときの輪講は、石原が担当していたんだったな。
　一宮に詰め寄られ、石原は慌てたように弁解した。
「ちょっと、なんですか。一宮さん。今さらそんな大昔の計算の話を持ち出さないでくださいよ。あのとき、このテキストには、こんな親切な図はまったく描いていなかったんです。それに、僕の積分路の変形が著者の意図と違ったものであったとしても、停留値を通る積分路なら、結論は同じになったはずです」
　石原は必死で弁解するように言った。
　なんだかこいつには、反省の色というものが微塵も感じられないな。

「ま、いいわ。昔のことを今さらほじくり返しても仕方がないわね」
　突然興味をなくしたように、一宮がくるりと背を向けた。
　石原はほっとしたように安堵のため息を漏らした。

　まあ、たしかに、『push the contour upward』と書いてあるだけじゃ、何を言ってるのかさっぱり分からないよな。
　その一方で、第２章には、積分路の変形を描いた図2.3が記載されていたりする。
　こういう理不尽な不親切さが、この場の量子論のテキストを必要以上に超絶難解にしているのかもしれないな。