ラグランジアンの物理的な意味 - スーパーサイエンスガール

　次のセクションからは、越野さんが再び解説を行うこととなった。
「セクション2.2では、場の量子論の議論で必要となる古典的な場の理論の定式化を見てみます。では、最初に、ラグランジュの場の理論を見てみましょう。古典力学の基本的な量は、作用Sと呼ばれる量であり、これはラグランジアンLの時間積分で表されます」
　一宮が手をあげた。
「何でしょうか、一宮さん」
「ラグランジアンって何よ？」
　
「ラグランジアン（Lagrangian）は、ラグランジュ関数とも呼ばれ、運動エネルギーTとポテンシャルエネルギーVの差を一般化座標 $\{q_k\}$ とその時間微分 $\{\dot{q}_k\}$ で表した関数です」

ラグランジアン（ラグランジュ関数）
${ \displaystyle \begin{eqnarray} L(q, \dot{q}, t)&=&T（運動エネルギー）-V（ポテンシャルエネルギー） \end{eqnarray} }$

　一宮は、訳が分からないといったように首を振った。
「どうしてそんな関数を考えるのよ？」
「ラグランジアンLから粒子の運動方程式を導くことができるからです」
「運動方程式が導けるって？」
　越野さんは頷いた。

「例えば、時刻 $t_0$ に位置 $x_0$ にあった粒子が、 $t_1$ に位置 $x_1$ に移動した場合を考えてみます。このとき、位置 $x_0$ と $x_1$ の間を結ぶ運動は、力学的エネルギー保存則が成立する保存系では、ラグランジアンLの時間積分S（作用積分）を用いて次のようにあらわすことができます」

${ \displaystyle \begin{eqnarray} dS&=&\delta\int_{t_0}^{t_1}L(q, \dot{q}, t)dt=0 \end{eqnarray} }$

「この式は、位置 $x_0$ と $x_1$ の間を通るさまざまな経路のうち、作用積分Sの変分がゼロ、すなわちラグランジアンLの変動が最小（極値）となるような経路に沿った運動のみが実現されることを意味し、このような原理を最小作用の原理と呼びます」

位置 $x_0$ と $x_1$ の間を通るさまざまな経路のうち、作用積分Sの変分がゼロ、すなわちラグランジアンLの変動が最小（極値）となるような経路に沿った運動のみが実現される

「実際、最小作用の原理は、運動方程式と等価であることが知られています」

最小作用の原理は、運動方程式と等価である

「でも、どうしてラグランジアンLの変動が最小になると、運動方程式と等価なのよ？」

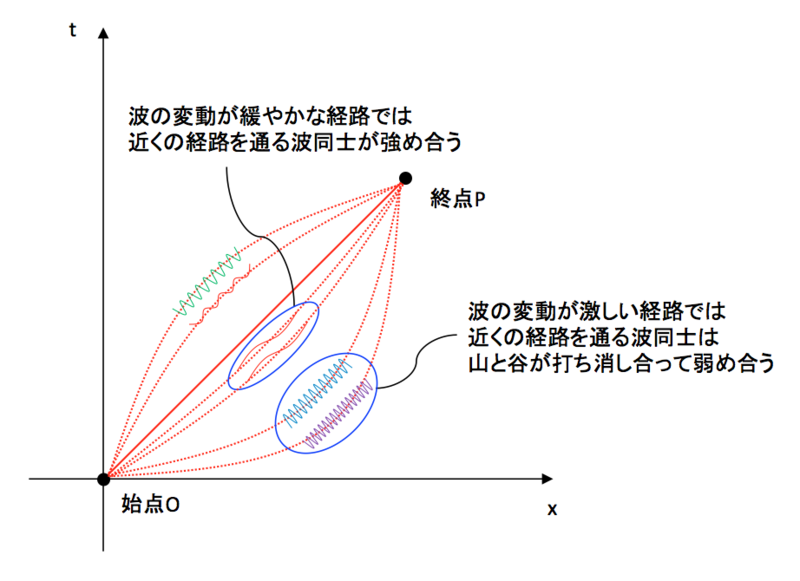
「それを理解するには、古典的な粒子のイメージではなく、量子力学的な波動のイメージで考える必要があります。量子力学的には、粒子の本質は波動であり、ある地点（始点O）から別の地点（終点P）まで粒子が移動するとき、その移動経路は１つではなく、実際には、下図のように、始点Oから終点Pまでの『無数の経路』を量子力学的な波動が伝播しているものと考えます」

粒子の本質は波動であり、始点Oから終点Pまでの経路を通る粒子は、１つの経路ではなく、実際には、下図のようなさまざまな経路を波動として伝搬している。

「ただし、上図に示されるように、それぞれの経路を通る波は同じように振動せず、その波の振動は、作用積分Sに依存することが知られています。量子力学的には、始点Oから終点Pまでの遷移振幅は、作用積分Sを用いて次のように、始点Oから終点Pに至るあらゆる経路を通る波の寄与の和として書くことができます（Aは係数）」

始点Oから終点Pまでの遷移振幅
${ \displaystyle \begin{eqnarray} U_{O\rightarrow P}&=&\Sigma_{OからPに至るあらゆる経路}A \exp{(iS)} \end{eqnarray} }$

「ここで、作用積分Sが最小の経路を通る波の変動は緩やかなため、近くの経路を通る波と強め合いますが、作用積分Sが大きな経路を通る波の変動は激しいため、近くの経路を通る波と山と谷が打ち消し合って弱め合います。その結果、作用積分Sが大きな経路を通る波の寄与は打ち消し合って消滅してしまい、作用積分Sが最小となる経路を通る波の寄与だけが強め合って最終的に残ります。この残った経路が、ちょうど古典的な粒子の運動方程式の経路と一致するのです」

ラグランジアンLの物理的な意味
波の振動は、ラグランジアンLの時間積分（作用積分S）に依存する
　↓
作用積分Sが最小の経路を通る波の変動は緩やか→近くの経路を通る波と強め合う
作用積分Sが大きな経路を通る波の変動は激しい→近くの経路を通る波と山と谷が打ち消し合って弱め合う
　↓
作用積分Sが大きな経路を通る波の寄与が打ち消し合って消滅し、作用積分Sが最小となる経路を通る波の寄与だけが最終的に残る
　↓
粒子の運動方程式の経路と一致

「これは、以前にお話した停留値法の考え方と似ています。このように、ラグランジアンは、波の振動の振る舞いを決定する基本的な量であり、粒子が波動であると考えることによって、その本質を理解することができるのです」