ファインマン処方を導入する理由 - スーパーサイエンスガール

「ところで、そもそもなんでファインマン処方なんてものを導入したのよ？」
　一宮がじろりと越野さんを睨み付けた。
「え？　ファインマン処方を導入した理由ですか？　そうですね……ファンマン処方がない場合、下図のように実軸上に極が位置するため、積分経路を実軸上からずらさないといけません」

f:id:Dreistein:20150725100135p:plain

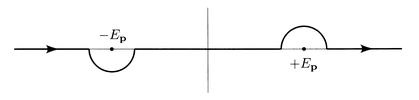
「でも、ファインマン処方を行うことで、下図に示すように、極の位置が実軸上から上下にずれるので、積分経路は原点を通る直線で表すことができます。だから、積分経路を上のように変形させる必要がなくなります」

f:id:Dreistein:20150712120448p:plain

「つまり、積分経路がシンプルになるというわけね」
　一宮は納得するように頷いた。
「でも、どうして $+E_{\bf{p}}$ の極が下側にずれて、 $-E_{\bf{p}}$ の極が上側にずれるのよ？　他のずれ方でもいいじゃない？　例えば、 $+E_{\bf{p}}$ の極が上側にずれて、 $-E_{\bf{p}}$ の極が下側にずれるとか？」
「それにはちゃんとした理由があります。 $x_0>y_0$ のとき、積分経路Cは下側の半円を通ることは以前お話ししましたよね」

f:id:Dreistein:20150712120339p:plain

「ここで、 $x^0-y^0=t$ と書けることからもわかるように、 $x^0>y^0$ というのは、 $t=x_0-y_0>0$ の場合、すなわち時間 $t$ が正（ $t>0$ ）の場合に相当し、このとき時間 $t$ は過去から未来に流れます」

$x^0-y^0=t$ （時間）
　↓
$x^0>y^0$ のとき、時間 $t$ は正（ $t=x_0-y_0>0$ ）となる
（このとき、時間は、過去から未来に流れる）

「ここで、積分経路C内に含まれる極のみが積分計算に寄与することを考えると、 $x^0>y^0$ のとき、すなわち時間が過去から未来に流れるときは、クライン‐ゴルドン粒子のエネルギーは正のエネルギー $E_{\bf{p}}$ （ $-i\epsilon$ は微小な値なので無視しました）となります」

積分経路C内に含まれる極のみが積分計算に寄与する
　↓
$x^0>y^0$ （時間が過去から未来に流れる）とき、クライン‐ゴルドン粒子のエネルギーは $E_{\bf{p}}$ となる

「つまり、正のエネルギーが過去から未来へと伝播しているというわけね」
　越野さんは頷いた。
「だから、エネルギーがプラスの極 $E_{\bf{p}}$ は、実軸より下側に来ないといけません。一方、 $x^0{<}y^0$ のときは、時間 $t$ は負（ $t=x_0-y_0{<}0$ ）となります」

$x^0{<}y^0$ のとき、時間 $t$ は負（ $t=x_0-y_0{<}0$ ）となる
（このとき、時間は、未来から過去に流れる）

f:id:Dreistein:20150712120323p:plain

「 $x^0{<}y^0$ のとき、すなわち時間が未来から過去に流れるときは、クライン‐ゴルドン粒子のエネルギーは負のエネルギー $-E_{\bf{p}}$ （ $+i\epsilon$ は微小な値なので無視しました）となります」
「つまり、時間が逆行（ $t{<}0$ ）するとき、負のエネルギー $-E_{\bf{p}}$ が未来から過去に流れることになるというわけね」

極 $E_{\bf{p}}$ が実軸の下側に来る→正のエネルギー $-E_{\bf{p}}$ が過去から未来に流れる
極 $-E_{\bf{p}}$ が実軸の上側に来る→負のエネルギー $-E_{\bf{p}}$ が未来から過去に流れる

「このように、極 $\pm E_{\bf{p}}$ が実軸の下側に来るか、あるいは上側に来るかで、エネルギーの流れと時間の流れの関係が決まります。一方、ファインマン処方を行わない場合、エネルギーの流れが時間の流れと矛盾しないように積分経路を指定する必要がありますが、以前もお話したように、このような積分経路は下図のように４つもあります」

f:id:Dreistein:20150725075240p:plain

「ファインマン処方はこのような面倒な積分経路の指定をせずとも、エネルギーの流れと時間の流れの関係を適切に設定できる点で優れているのです」