留数定理による複素積分の計算 - スーパーサイエンスガール

${ \displaystyle \begin{eqnarray} &&_{x^0>y^0}\int\frac{d^3p}{(2\pi)^3}\int\frac{dp^0}{2\pi i}\frac{-1}{p^2-m^2} e^{-ip\cdot (x-y)}\\ &=&_{x^0>y^0}\int\frac{d^3p}{(2\pi)^3}\int\frac{dp^0}{2\pi i}\frac{-1}{(p^0+ E_{\bf{p}}) (p^0- E_{\bf{p}})} e^{-ip\cdot (x-y)}. \end{eqnarray} }$

「次に、積分 $p^0$ の被積分関数を $f(z)$ として、実際に、留数 $\textrm{Res}[f, \pm E_p]$ を求めてみましょう」

被積分関数
${ \displaystyle \begin{eqnarray} f(z)=\frac{1}{2\pi i}\frac{-1}{(z+ E_{\bf{p}}) (z- E_{\bf{p}})} e^{-iz\cdot (x_0-y_0)} \end{eqnarray} }$

「 $z=\pm E_{\bf{p}}$ は１位の極なので、留数 $\textrm{Res}[f, \pm E_p]$ は次の関係から求めることができます」

${ \displaystyle \begin{eqnarray} \textrm{Res}[f, a]=\lim_{z\rightarrow a}(z-a)f(z) \end{eqnarray} }$

「 $a=\pm E_p$ として、上の関係式から留数 $\textrm{Res}[f, \pm E_p]$ を求めてみます」

${ \displaystyle \begin{eqnarray} \textrm{Res}[f, \pm E_p]&=&\lim_{z\rightarrow \pm E_p}(z \mp E_p)f(z)\\ &=&\lim_{z\rightarrow \pm E_p}(z\mp E_p)\frac{1}{2\pi i}\frac{-1}{(z+ E_{\bf{p}}) (z- E_{\bf{p}})} e^{-iz\cdot (x_0-y_0)}\\ &=&\lim_{z\rightarrow \pm E_p}\frac{1}{2\pi i}\frac{-1}{(z\pm E_{\bf{p}})} e^{-iz\cdot (x_0-y_0)}\\ &=&\frac{1}{2\pi i}\frac{-1}{\pm 2E_{\bf{p}}} e^{\mp iE_{\bf{p}}\cdot (x_0-y_0)} \end{eqnarray} }$

「したがって、留数定理から $p^0$ の積分を求めることができます」

留数定理
${ \displaystyle \begin{eqnarray} \frac{1}{2\pi i}\int_c f(z)dz=\textrm{Res}[f, a_1]+\textrm{Res}[f, a_2]+\cdots+\textrm{Res}[f, a_m] \end{eqnarray} }$

「上で求めた留数 $\textrm{Res}[f, \pm E_p]$ を留数定理に代入します。ただし、積分経路Cは、 $p^0= \pm E_{\bf{p}}$ の極を反時計回りでなく、時計回りに囲っているので、全体としてマイナスの符号が付くことに注意してください」

f:id:Dreistein:20150628065118p:plain

${ \displaystyle \begin{eqnarray} \frac{1}{2\pi i}\int_c f(z)dz&=&-\big(\textrm{Res}[f, E_p]+\textrm{Res}[f, -E_p]\big)\\ \int_c f(z)dz&=&-2\pi i\big(\textrm{Res}[f, E_p]+\textrm{Res}[f, -E_p]\big)\\ &=&-2\pi i\bigg(\frac{1}{2\pi i}\frac{-1}{2E_{\bf{p}}} e^{ -iE_{\bf{p}}\cdot (x_0-y_0)}+\frac{1}{2\pi i}\frac{-1}{-2E_{\bf{p}}} e^{iE_{\bf{p}}\cdot (x_0-y_0)}\bigg)\\ &=&\frac{1}{2E_{\bf{p}}} e^{ -iE_{\bf{p}}\cdot (x_0-y_0)}+\frac{1}{-2E_{\bf{p}}} e^{iE_{\bf{p}}\cdot (x_0-y_0)}\\ &=&\frac{1}{2E_{\bf{p}}} e^{ -ip_0\cdot (x_0-y_0)}\bigg|_{p_0=E_{\bf{p}}}+\frac{1}{-2E_{\bf{p}}} e^{-ip_0\cdot (x_0-y_0)}\bigg|_{p_0=-E_{\bf{p}}} \end{eqnarray} }$

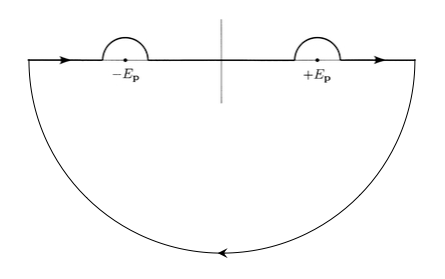
「これから、下の(2.54)式の最後の行において、 $\int dp^0$ を複素積分 $\int_C z$ に拡張して、上式を代入することによって、(2.54)式の２行目の式を導くことができるというわけです」

${ \displaystyle \begin{eqnarray} \langle 0\mid [\phi(x), \phi(y)]\mid 0\rangle&=&\int\frac{d^3p}{(2\pi)^3}\frac{1}{2E_{\bf{p}}}\big(e^{-ip\cdot (x-y)}-e^{ip\cdot (x-y)}\big)\\ &=&\int\frac{d^3p}{(2\pi)^3} \bigg\{\frac{1}{2E_{\bf{p}}}e^{-ip\cdot (x-y)}\bigg|_{p^0=E_{\bf{p}}}\\ &&\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{1}{-2E_{\bf{p}}}e^{-ip\cdot (x-y)}\bigg|_{p^0=-E_{\bf{p}}}\bigg\}\\ &=&_{x^0>y^0}\int\frac{d^3p}{(2\pi)^3}\int\frac{dp^0}{2\pi i}\frac{-1}{p^2-m^2} e^{-ip\cdot (x-y)}. \end{eqnarray} }$
(2.54)

「以上が、(2.54)式の行間の計算の説明です」